# 최대 유량 알고리즘 (Maximum Flow Algorithm) 이란?
그래프에서 두 정점 사이에 얼마나 많은 "유량(flow)"을 보낼 수 있는지 계산하는 알고리즘을 말한다.
ex)

다음과 같이 방향이 있는 그래프를 파이프 망이라고 생각해 보자.
이때 간선은 파이프, 정점은 분기점이다.
각 간선은 파이프에 용량만큼, 가중치를 가진다.
그때 물이 흐른다면, 파이프 망을 통해 흐르는 물의 양의 최대는 무엇일까?
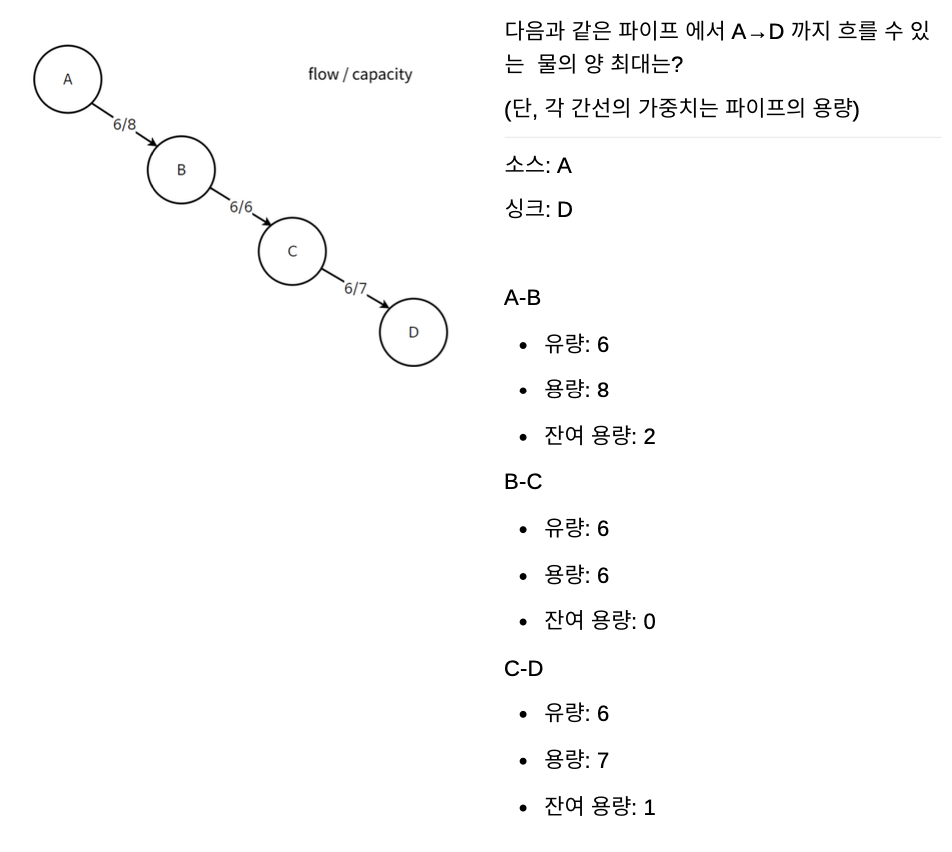
다음과 같은 파이프에서 A→D 까지 흐를 수 있는 물의 양 최대는?
A. 정답은 6!
B-C의 용량이 경로에서 가장 적은 용량(6)이기 때문에 병목현상으로 더 많은 물을 흘릴 수 없다.
# 용어
| 유량(Flow) | f(u, v)는 정점 u에서 v로의 간선에 실제로 흐르는 유량을 의미 |
| 용량(Capacity) | c(u, v)는 정점 u에서 v로 가는 간선의 용량(가중치) |
| 잔여 용량(Residual Capacity) | 해당 간선에 추가적으로 더 흘려 보낼 수 있는 유량 간선의 용량과 유량의 차이 r(u, v) = c(u, v) - f(u, v) |
| 소스(source) | 유량이 시작되는 정점(출발지) |
| 싱크(sink) | 모든 유량이 도착하는 정점(도착지) |
모든 유량은 소스(source)에서 싱크(sink)로 흐른다.
네트워크 플로우는 소스(source)에서 싱크(sink)로 흐를 수 있는 최대 유량을 계산하는 알고리즘!
# 속성
용량 제한 속성 : f(u, v) <= c(u, v)
각 간선의 유량은 해당 간선의 용량을 초과할 수 없다.
유량의 대칭성 : f(u, v) = -f(v, u)
음의 유량이라는 가상의 유량이 있다고 가정한다.
u에서 v로 유량이 흘러올 경우, v의 입장에서는 u로 음수의 유량을 보내는 것이라고 생각한다.
음의 유량을 통해 잔여 용량을 만들어, 추가적인 경로를 탐색할 수 있다.
유량 보존의 법칙 : ∑f(u, v) = 0
Source와 Sink를 제외한 모든 각 정점에 대해서 들어오는 유량과 나가는 유량의 양은 같다.유량의 대칭성에 의해 한 정점의 모든 유량의 합은 0 이다.
# 포드-풀커슨 기법
모든 간선의 유량을 0으로 시작하여 소스에서 싱크로의 경로 중 증가 경로(augmenting path)를 찾아 유량을 흘려보내기를 반복한다.
증가 경로(augmenting path)란?
=> 유량을 흘려보내기 위해 찾은 경로
증가 경로에 흐를 수 있는 유량 = 경로에 포함되는 간선들의 잔여 용량 중 최솟값
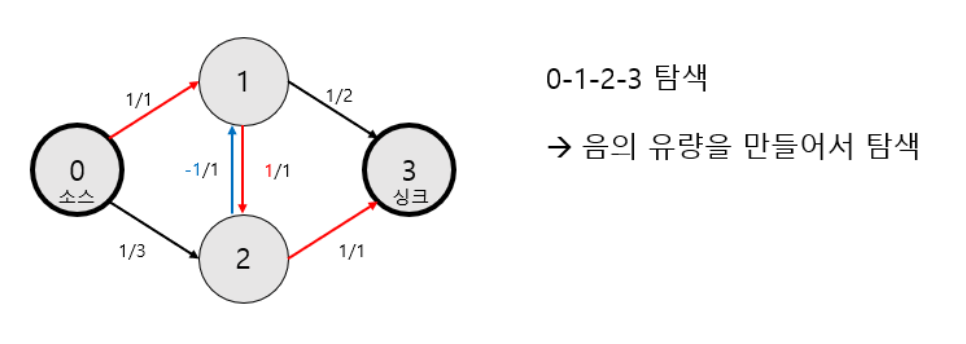
ex) 아래 그림과 같은 그래프가 있다. 최대 유량을 구해보자.

차례로 경로를 탐색해 경로의 최대 유량을 흘려보내준다.



이처럼 경로를 탐색하는 순서에 의해 최대 유량을 구하지 못할 가능성이 생긴다.
해결 방법은 음의 유량을 만드는 것이다. 이는, 잘못 간 경로를 취소하고 새로운 경로를 찾을 수 있게 한다.
💡 유량의 대칭성 : 음의 유량을 만들어서 새로운 경로를 탐색할 수 있게 한다. f(u, v) = -f(u, v)
# 에드몬드-카프 알고리즘
포드 풀커슨 기법을 BFS를 사용하여 구하는 알고리즘으로, BFS로 모든 경로를 찾아서 남아있는 용량을 흘려보내는 것을 반복한다.
시간 복잡도: O(VE^2)
-> BFS를 O(VE)번 수행한다.
수행 과정
while(1) {
1. BFS로 소스에서 싱크까지의 경로를 구한다.
- 단, 경로는 잔여 용량이 있어 지나갈 수 있어야 한다.
- 지나갈 수 있는 경로가 없으면 탈출한다.
종결 조건 (더 이상 증가 경로를 찾을 수 없다.)
2. 유량 구하기
- 증가 경로에서 흐를 수 있는 용량 구하기 (경로에 포함되는 간선들의 잔여 용량 중 최솟값)
- 경로를 따라 유량을 추가한다. (음의 유량, 양의 유량)
}
코드
vector<int> adj[500]; // 인접 행렬
int c[500][500] // 용량
int f[500][500]; // 현재 유량
int visit[500]; // 방문 배열 (경로를 저장하는 배열 -> parent를 기록)
int result = 0; // 결과 저장
void NetworkFlow(int start, int end) {
while (1) {
fill(visit, visit+n+1, -1);
// BFS -> sink로 도달하는 경로를 찾는다.
queue<int> q;
q.push(start);
while (!q.empty()) {
int x = q.front();
q.pop();
for (int i = 0;i < adj[x].size();i++) {
int y = adj[x][i];
// 방문하지 않은 노드 중 용량이 남는 경우
if (c[x][y] - f[x][y] > 0 && visit[y] == -1) {
q.push(y);
visit[y] = x;
if (y == end) break;
}
}
}
// 종결
if (visit[end] == -1) break;
//------ 유량 구하기 ------//
int flow = INF;
// 증가 경로에서 흐를 수 있는 유량 구하기 (경로에 포함되는 간선들의 잔여 용량 중 최솟값)
for (int i = end;i != start;i = visit[i])
flow = min(flow, c[visit[i]][i] - f[visit[i]][i]);
// 경로를 따라 유량 추가
for (int i = end;i != start;i = visit[i]) {
f[visit[i]][i] += flow; // 양의 유량
f[i][visit[i]] -= flow; // 음의 유량
}
result += flow;
}
}
# 기본 문제
'알고리즘 > 알고리즘 이론' 카테고리의 다른 글
| Monotone Stack, Monotone Queue (단조 스택, 단조 큐) (1) | 2023.11.06 |
|---|---|
| 포함 배제의 원리 (Inclusion-Exclusion Principle) (1) | 2023.10.23 |
| Disjoint set, 분리 집합, Union-Find (0) | 2022.03.08 |
| 탐색 알고리즘(DFS, BFS)과 활용 (0) | 2022.03.05 |
| 냅색(Knapsack) 알고리즘 (0) | 2022.03.04 |